C program to find out the total number of subarray having product less than a value :
In this tutorial, we will learn how to find the total number of subarray with product less than a specific value. For example, lets take a look at the array 9,5,4,7,2. Suppose, we are checking for subarray with product less than 50. We will have the following subarrays :
- [9] since 9 < 50
- [9,5] since 9*5 = 45 < 50
- [9,5,4]
- [5]
- [5,4]
- [4]
- [4,7]
- [7]
- [7,2]
i.e. total 9 different subarrays. To solve this problem, we will learn two different approach.
Approach 1 :
In this method, we will use two different for loops to find out the subarrays. Let’s take a look at the below image :
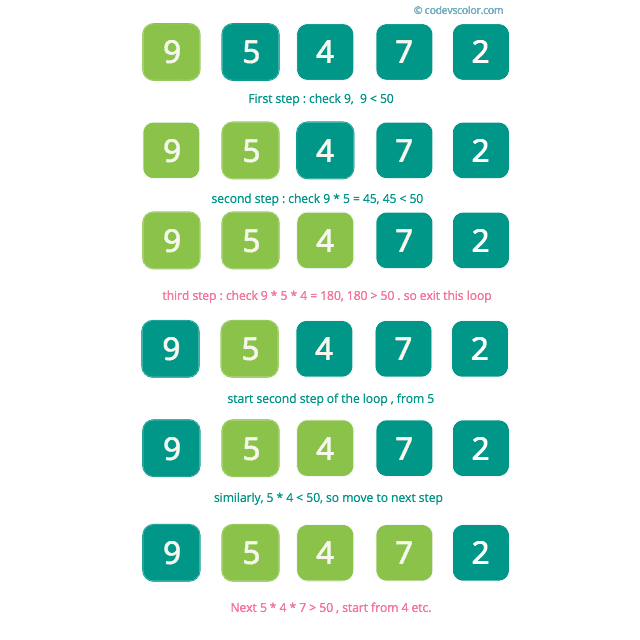
- Start from the first index of the array.
- Check if the element is less than total product or not. If yes, increment the count.
- Move to the next element and find the product again, i.e. first element and second element product.
- Check if the product is less than or not, if yes, increment the count. Similarly, check one by one element of the array.
- If at some point, the product becomes more than the value, move to the second element and check all elements right to it similarly.
Following C program will explain the process we have discussed above :
#include <stdio.h>
int main()
{
int myArray[] = {9,5,4,7,2};
int product = 50;
int count = 0;
int i,j;
int currentProduct;
int arrayLength = sizeof(myArray)/sizeof(myArray[0]);
for(i = 0; i< arrayLength; i++){
if(myArray[i] < product){
count ++;
currentProduct = myArray[i];
for(j=i+1; j < arrayLength; j++){
currentProduct = currentProduct * myArray[j];
if(currentProduct < product){
count++;
}else{
break;
}
}
}else{
continue;
}
}
printf("Total count : %d",count);
}
It will print out 9 as the output.The complexity is O(n^2)
Process 2 : Sliding window technique :
We will use one window or a continuous series of number at one time. We will use the same array used in the program above. The window will keep increasing till the product becomes more than the given value. If it will increase the value, we will remove one element from the left and then add more elements again. For each subarray, new added elements will be endIndex - startIndex.endIndex will start from 1 and startIndex will from 0. To understand this problem, take a look at the below image first :
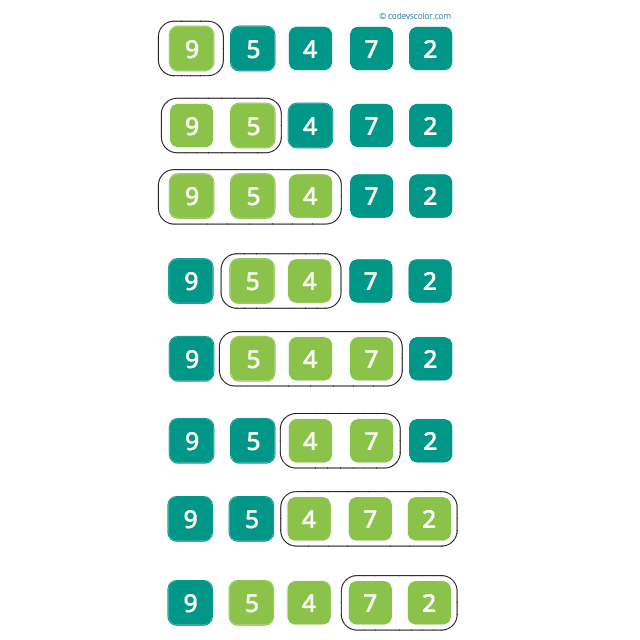
The start index is 0 and the end index is 1 at first.
- First start with the first number. Since 9 < 50 , count = 1. Subarrays : [9]
- Add the second number. 9 * 5 = 45 < 50, count = count + (endIndex-startIndex) = 1 + (2-0) 3. Subarrays : [9],[9,5],[5]
- Add the next number . 9 * 5 * 4 > 50. So, remove the start element from the subarray.
- count = count + (3-1) = 3 + 2 = 5. Subarrays : [9], [9,5] ,[5] ,[5,4], [4].
- 5 * 4 * 7 > 50, so move to the next step.
- count = count + (4-2) = 7. Subarrays : [9], [9,5], [5], [5,4], [4], [4,7], [7].
- 4 * 7 * 2 > 50 , skip.
- count = count + (5-3) = 9. Subarrays : [9], [9,5], [5], [5,4], [4], [4,7], [7], [7,2], [2]
Now, Let’s try to implement this in C :
#include <stdio.h>
int main()
{
int myArray[] = {9,5,4,7,2};
int startIndex = 0;
int endIndex = 1;
int currentProduct = myArray[0];
int count = 0;
int max = 50;
int length = sizeof(myArray)/sizeof(myArray[0]);
while(startIndex < endIndex && endIndex <= length){
if(currentProduct < max){
count = count + (endIndex - startIndex);
if(endIndex != length){
currentProduct = currentProduct * myArray[endIndex];
}
endIndex++;
}else{
currentProduct = currentProduct / myArray[startIndex];
startIndex ++;
}
}
printf("Total count : %d ",count);
}
The complexity of this program is O(n) and it will print 9 as the output.
