Introduction :
In this C++ program, we will learn how to check if a number is power of 2 or not using its binary representation. The first method will use bitwise AND operation and the second one will count the number of 1 in its binary form.
Method 1: Using bitwise operation :
Let’s take a look at the binary representation of 0 to 16.
0 0
1 1 *
2 10 *
3 11
4 100 *
5 101
6 110
7 111
8 1000 *
9 1001
10 1010
11 1011
12 1100
13 1101
14 1110
15 1111
16 10000 *
The rows with star marked are the rows for the power of 2. As you can see here, if a number is n power of 2, its binary representation will be 1 followed by n times 0. For example, 16 is 2 to the power 4. So, its binary representation is 10000 or 1 followed by 4 zeros.
One more thing to notice here is that the number prior to the power of 2 has its binary representation with only 1. Check 1, 7 and 15 in the above list. 0 is an exception here.
Using the above two concepts, we can find out if a number is the power of two or not using a single logical AND operation. If a number is the power of 2, we can do one logical AND with the number and the previous number and the result will be 0 always. For example :
15 : 0 1 1 1 1
16 : 1 0 0 0 0
--------------
& : 0 0 0 0 0
Here, the logical AND of 15 and 16 is 0.
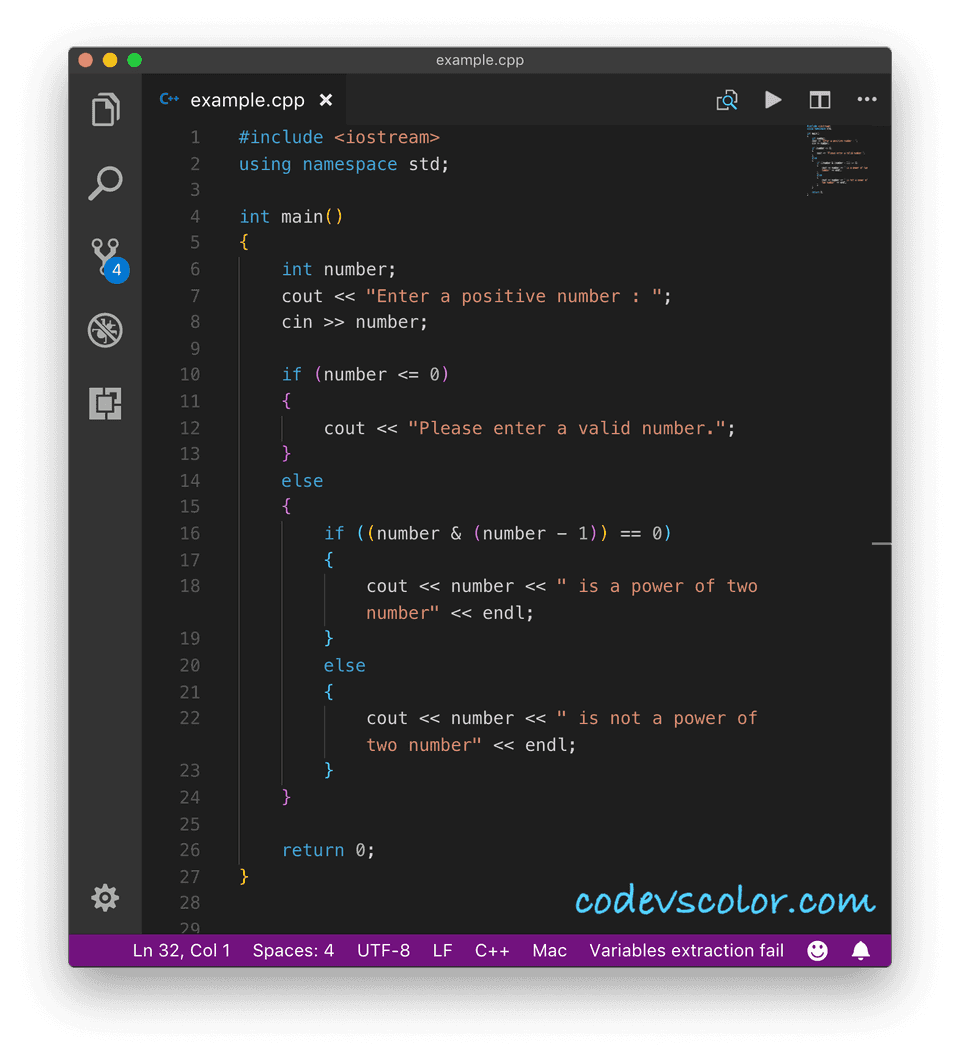
C++ program :
In C++, for AND operation, & is used. We can write the above logic in code like below :
#include <iostream>
using namespace std;
int main()
{
int number;
cout << "Enter a positive number : "; cin >> number;
if (number <= 0)
{
cout << "Please enter a valid number.";
}
else
{
if ((number & (number - 1)) == 0)
{
cout << number << " is a power of two number" << endl;
}
else
{
cout << number << " is not a power of two number" << endl;
}
}
return 0;
}
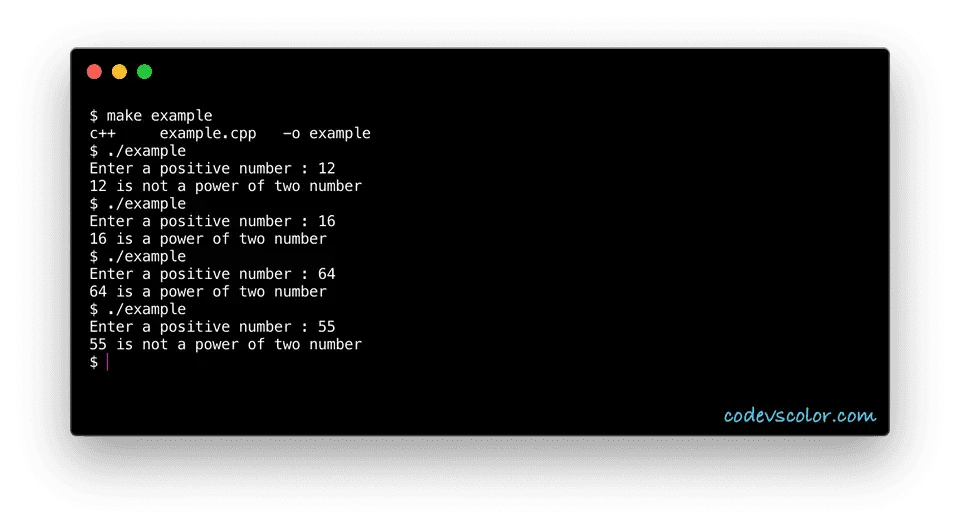
Sample Output :
Enter a positive number : 16
16 is a power of two number
Enter a positive number : 22
16 is not a power of two number
Method 2: By counting the number of 1 in its binary form :
We have seen before that if a number is the power of two, it has only one 1 in its binary form. So, we can calculate the total number of 1 in its binary to find out if it is the power of two or not.
The easiest way to calculate the total number of 1 is to keep calculating the AND of the number and its previous number until the result is 0. The number of steps required to get 0 is the total number of 1.
C++ program :
#include <iostream>
using namespace std;
int main()
{
int number;
cout << "Enter a positive number : "; cin >> number;
if (number <= 0)
{
cout << "Please enter a valid number.";
}
else
{
int count = 0;
while(number != 0){
number = number & (number - 1);
count ++;
}
cout << count<<endl;
if (count == 1)
{
cout << "It is a power of two" << endl;
}
else
{
cout << "It is not a power of two" << endl;
}
}
return 0;
}
Actually, this is the same as the first method. If the value of count is greater than 1 in the while loop, we can just skip and say that this is not a power of two. In the previous solution, we were checking if the AND of a number and its previous number is 0 or not i.e. if the value of count is 1 or not as per the second solution.
It will give the same result for a number as the first solution.
Conclusion :
We have learned two different ways to verify if a number is the power of two or not. Try to run these examples on your machine and drop one comment below if you have any queries.