3 Different ways to print Pascal’s triangle in Java:
In this post, we will learn different ways to print Pascal’s triangle in Java. Pascal’s triangle is a triangle or number. This is named after French mathematician Blaise Pascal.
Example of Pascal’s triangle:
Let me show you an example of Pascal’s triangle:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1This is a Pascal’s triangle of height 5.
You can see that:
- Each digit in a row is the sum of the left and right digits of its previous row.
- The first and the last digit is 1 for each row.
We can use different algorithms to print a Pascal’s triangle. These algorithms works in a similar way, i.e. you can use these algorithms with any other programming languages.
Method 1: Java program to print a Pascal’s triangle using formula:
We can use a simple formula to print a Pascal’s triangle.
- Suppose, lastDigit is the last digit calculated for a row.
- i is the current row
- j is the current column
- Then, the current digit for [i,j] position is lastDigit*(i-j +1)/j
Also, we know that the first and the last digit of a Pascal’s triangle is 1. So, we can print 1 if the value of j is 0 or if i is equal to j.
We have to add blank spaces before the digits. Let me show you a Pascal’s triangle by replacing the spaces with *:
********* 1
******* 1 1
***** 1 2 1
*** 1 3 3 1
* 1 4 6 4 1This triangle has height 5. For each row, we are printing 2 * (height - row) number of *, if we consider the first row as 1. In the program, we will replace these with spaces.
Let’s write it down in Java:
import java.util.Scanner;
class Main {
public static void main(String[] args) {
int rows, digit = 1;
Scanner sc = new Scanner(System.in);
System.out.println("Enter the height of the triangle: ");
rows = sc.nextInt();
for (int i = 0; i < rows; i++) {
for (int j = 1; j < 2 * (rows - i); j++) {
System.out.print(" ");
}
for (int j = 0; j <= i; j++) {
if (j == 0 || i == j)
digit = 1;
else
digit = digit * (i - j + 1) / j;
System.out.format("%4d", digit);
}
System.out.println();
}
}
}Here,
- rows and digit are two integer values to hold the total rows count and the digit to print.
- sc is a Scanner object to read the user input value.
- It takes the height of the triangle as an input from the user and stores that in the rows variable.
- We are using three for loops here.
- The outer loop is to point to a row.
- The first inner loop is to print the spaces.
- The second inner loop is to print the digit.
- The outer loop runs from i = 0 to i = rows - 1.
- The first inner loop runs to print the spaces.
- The second loop prints the value of the digit. Before we print the value of digit, we are calculating its value. If j == 0 or i == j, it assigns 1 to digits. Else, it uses the formula we discussed above to calculate its value.
- We are using %4d to print the value to make sure that it doesn’t break the triangle for large digit value.
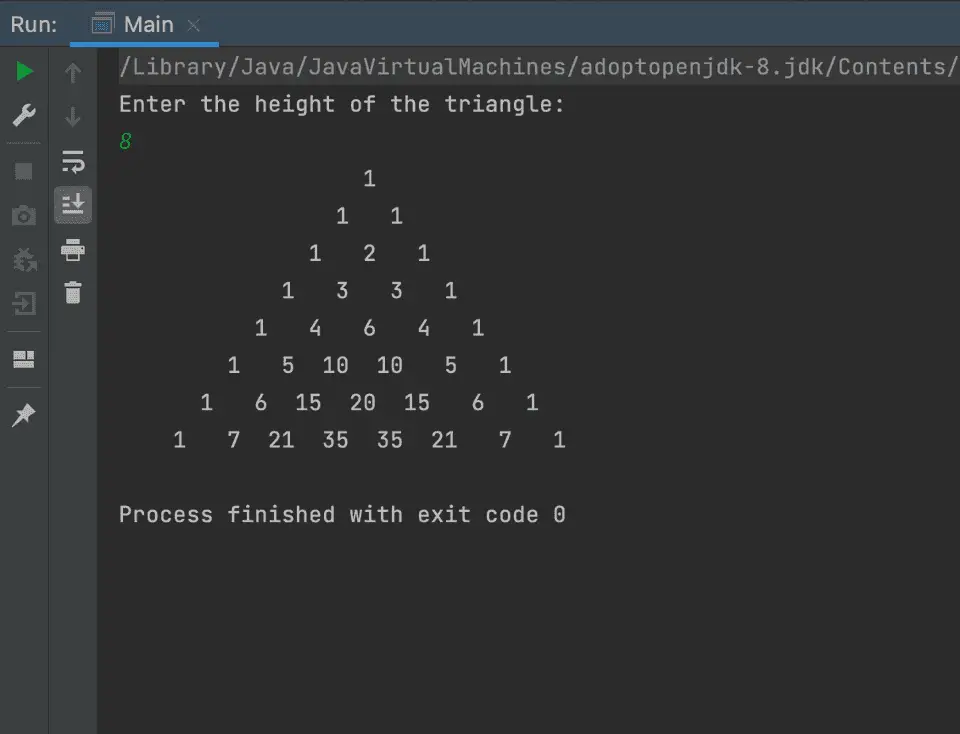
If you run this program, it will print output as like below:
Enter the height of the triangle:
8
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1Method 2: Java program to print a Pascal’s triangle using Combination:
We can also use combination to print the Pascal’s triangle. Each digit can be represent as rowCcol if row is the row count and col is the column count and both starts from 0.
For example, the fourth row is : 1 3 3 1. In combination, it is 3C0 3C1 3C2 3C3.
Below is the complete program:
import java.util.Scanner;
class Main {
public static int factorial(int n){
if (n == 1){
return 1;
}
return n * factorial(n - 1);
}
public static int nCr(int n, int r){
return factorial(n)/(factorial(n - r) * factorial(r));
}
public static void main(String[] args) {
int rows, digit = 1;
Scanner sc = new Scanner(System.in);
System.out.println("Enter the height of the triangle: ");
rows = sc.nextInt();
for (int i = 0; i < rows; i++) {
for (int j = 1; j < 2 * (rows - i); j++) {
System.out.print(" ");
}
for (int j = 0; j <= i; j++) {
if (j == 0 || i == j)
digit = 1;
else
digit = nCr(i, j);
System.out.format("%4d", digit);
}
System.out.println();
}
}
}Here,
- factorial is a method to find the factorial of a number. It takes a number and returns the factorial of that number.
- nCr is used to find the combination value. It uses the factorial method to find the combination.
- The other part of the program is same. The only difference is that we are using nCr instead of using the formula to find the digit at a specific position.
If you run this program, it will print similar result.
Enter the height of the triangle:
9
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1Method 3: Print the Pascal’s triangle by using extra space:
We can print a row by using the digits of the previous row. For a number at column value j, it is equal to the sum of at value j - 1 and j of the previous row. For the first and the last digit, we will print 1.
Below is the complete java program:
import java.util.ArrayList;
import java.util.Scanner;
class Main {
public static void main(String[] args) {
int rows, digit = 1;
Scanner sc = new Scanner(System.in);
ArrayList<Integer> prevRow = new ArrayList<>();
ArrayList<Integer> currentRow = new ArrayList<>();
System.out.println("Enter the height of the triangle: ");
rows = sc.nextInt();
for (int i = 0; i < rows; i++) {
for (int j = 1; j < 2 * (rows - i); j++) {
System.out.print(" ");
}
for (int j = 0; j <= i; j++) {
if (j == 0 || i == j)
digit = 1;
else
digit = prevRow.get(j - 1) + prevRow.get(j);
currentRow.add(digit);
System.out.format("%4d", digit);
}
prevRow = new ArrayList<Integer>(currentRow);
currentRow.clear();
System.out.println();
}
}
}Here,
- We are taking two arraylist to hold the current row and previous row data.
- While iterating through the elements of a row, we are adding it to currentRow arraylist.
- If the digit is not the first or the last digit, we are using the previous row arraylist to calculate the digit. It is the sum of the j - 1th item and jth item of the previous row.
- Once a row is printed, we are making a copy of currentRow and assigning it to prevRow. Also, clearing the currentRow arraylist.
If you run this program, it will give similar output:
Enter the height of the triangle:
8
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1You might also like:
- Java program to check if a number is a tech number or not
- How to import math class in Java example
- How to use pi value in Java with example
- Java program to check if a number is a ugly number or not
- Java program to check if a number is a unique number or not
- Java program to check if a number is Nelson number or not
- Java.util.Arrays.copyOf() method explanation with example