Named arguments in Kotlin :
Named argument is used to improve the readability of a kotlin function. Named argument, as the name suggested is arguments with a name. For example, let’s take a look at the below function :
fun calculateTotal(physics : Int,maths : Int,chemistry : Int): Int{
return physics + maths + chemistry;
}
If we have to call this function for physics = 88, maths = 87 and chemistry = 79, we can do that like below :
calculateTotal(88,87,79)
As you can see that the function is less readable. It will be more difficult to read for a function with a lot of arguments. Named argument was introduced to overcome this problem.
Example of Named argument :
Let’s try to use named argument for the example above :
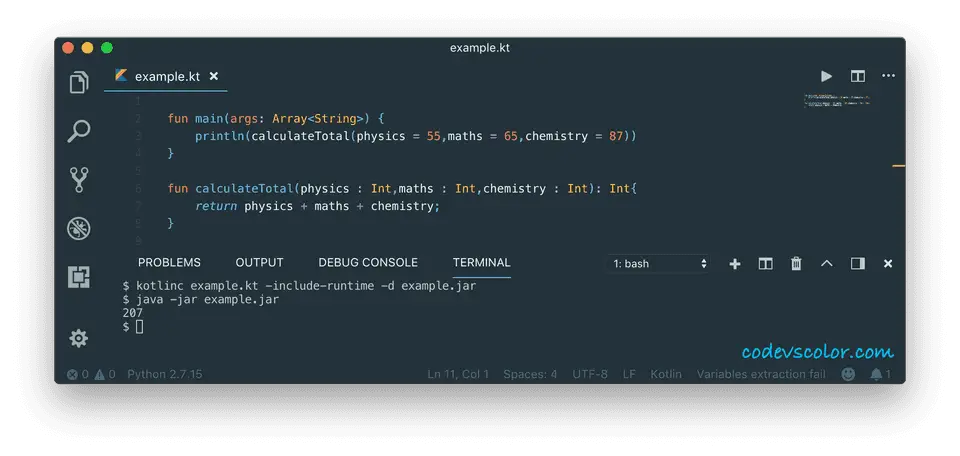
fun main(args: Array) {
println(calculateTotal(physics = 55,maths = 65,chemistry = 87))
}
fun calculateTotal(physics : Int,maths : Int,chemistry : Int): Int{
return physics + maths + chemistry;
}
It will print the below output :
207
As you can see that we have added the ‘names’ of each argument while calling the function. It makes the program more readable. We can also call the function without maintaining the order of the arguments like below :
println(calculateTotal(maths = 65,chemistry = 87,physics = 55))
That is one more advantage of named argument.
Named argument with a variable number of arguments :
Variable number of arguments can be used using the spread operator. For example :
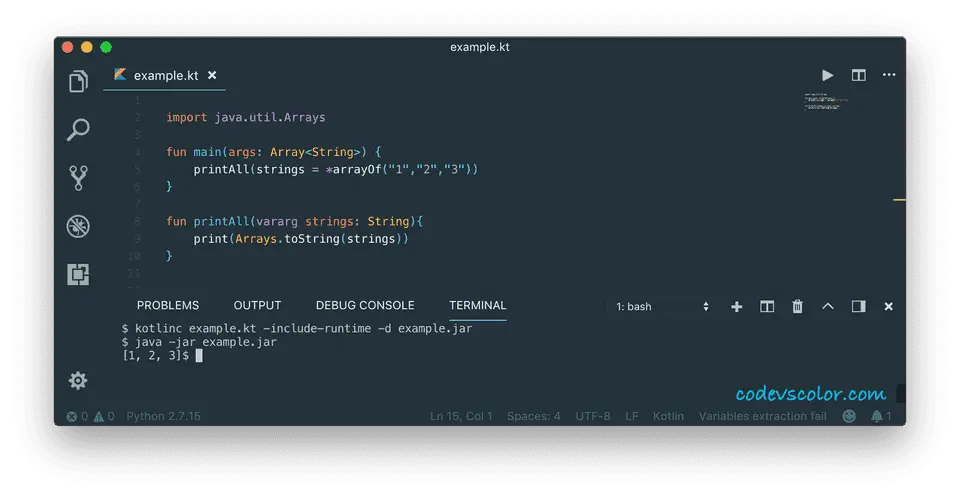
import java.util.Arrays
fun main(args: Array) {
printAll(strings = *arrayOf("1","2","3"))
}
fun printAll(vararg strings: String){
print(Arrays.toString(strings))
}
It will print the below output :
[1, 2, 3]