Python program to print an identity matrix :
In this tutorial, we will learn how to print an identity matrix in python. A matrix is called identity matrix if all of its diagonal elements from the upper left corner to bottom right corner is 1 and all other elements are 0. For example, the following matrices are “identity matrix” :
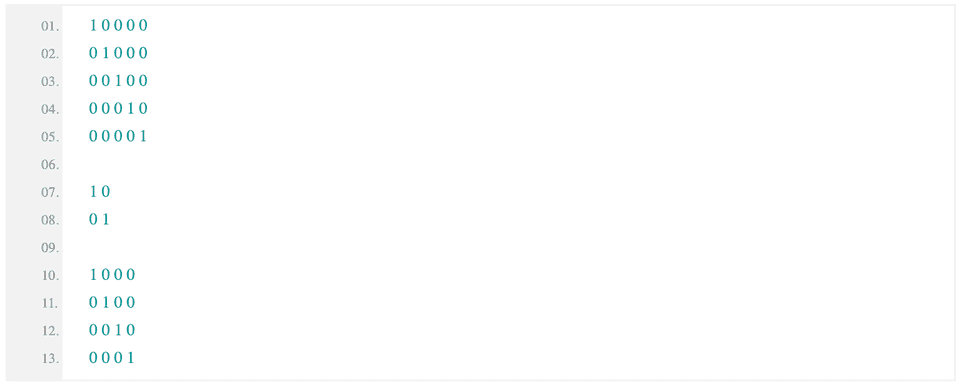
Two more terms we need to know about matrices are ‘row’ and ‘column’. If a matrix has m rows and n columns, it is called a (m x n) matrix. Note that the identity matrix is also known as the unit matrix. The row count is equal to the column count for an identity matrix.
So, instead of row and column, identity matrices are defined by its size. If the size is ’n’, it will have ’n’ number of rows and ’n’ number of columns. These types of matrices with equal row and column size are also called a square matrix.
In this tutorial, we will learn how to print an identity matrix using python.
In our program, we will ask the user to enter the size of the matrix and then we will print the identity matrix. As mentioned before, Let’s take a look at the program :
Python program :
#1
size = int(input("Enter the size of the matrix : "))
#2
for i in range(0,size):
#3
for j in range(0,size):
#4
if(i==j):
print("1",end = " ")
else:
print("0",end = " ")
#5
print()The source code is available here.
Explanation :
The main idea behind printing an identity matrix is that its value will be equal to 1 if the current row number is equal to the current column number. For first row, matrix[0][0] is 1, for the second row, matrix[1][1] is 1 etc. So, to print the matrix, we will use two for loops and if both the counters of both for loops is same, print 1. Else, print 0.
- The commented numbers in the above program denote the step number below :
Ask the user to enter the size of the matrix and save it in variable size. This will be the row and column size for the identity matrix.
-
Run one for loop from 0 to size of the matrix – 1. We are using this for loop for printing the rows of the matrix. If the current value in this loop is 0, that means we are working on the first row of the matrix, if it is 1, we are working on the second row of the matrix etc.
-
Start one more inner for loop and run it from 0 to size of the matrix – 1. This inner loop is used for working on the columns of the matrix. If the current value in this loop is 0, we are working on the first column of the matrix, if it is 1, we are working on the second column of the matrix etc. So, for any value of the outer loop, i.e. the loop on step-2, this inner loop will run completely. i.e. we will first print all column values for the first row, then for the second row etc.
-
Check if_ i_ is equal to_ j_ or not. If yes, print 1, else print 0. This step is used to print 1 in the diagonal of the matrix. We are printing 1, only if the current row index of the outer loop is equal to the column index of the inner loop.
-
Print one new line. Or move to the next row.


