Python program to solve the quadratic equation :
In this python programming tutorial, we will learn how to solve a quadratic equation. The user will enter the values of the equation, our program will solve it and print out the result. The quadratic equation is defined as below :
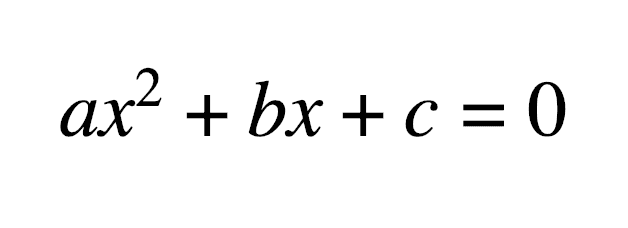
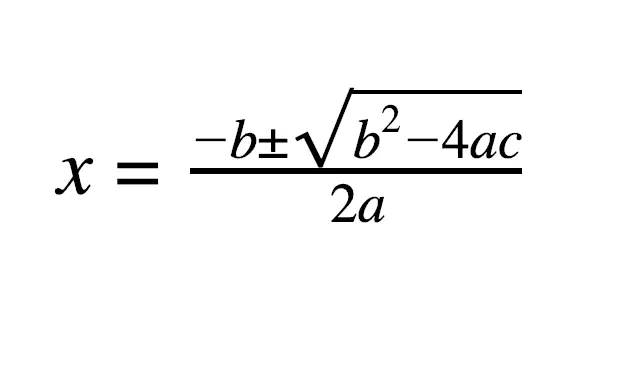
So, if we know the values of a,b and c, we can find out the value of_ ‘x’_. The _‘x’ _will have two values or we will have two solutions for any quadratic equation.
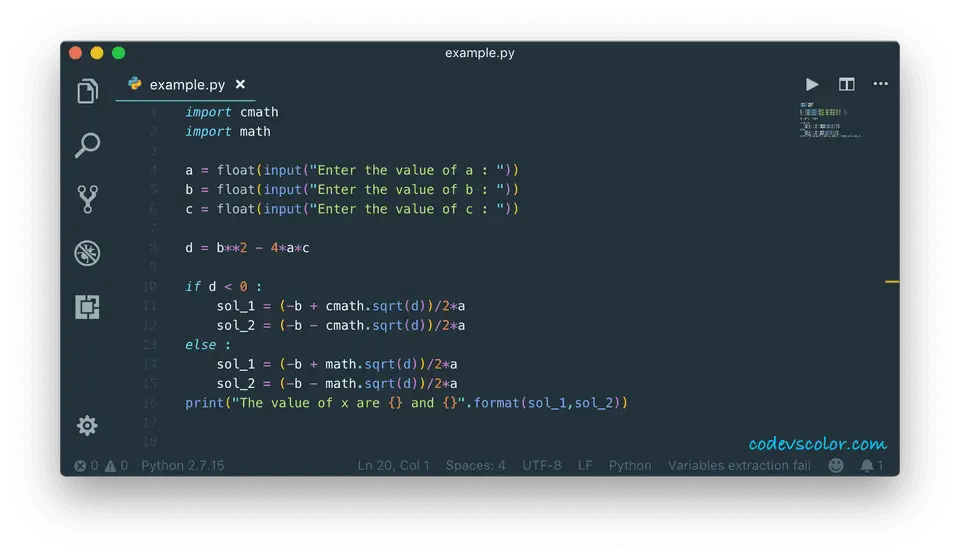
Python program :
#1
import cmath
import math
#2
a = float(input("Enter the value of a : "))
b = float(input("Enter the value of b : "))
c = float(input("Enter the value of c : "))
#3
d = b**2 - 4*a*c
#4
if d < 0 :
sol_1 = (-b + cmath.sqrt(d))/2*a
sol_2 = (-b - cmath.sqrt(d))/2*a
else :
sol_1 = (-b + math.sqrt(d))/2*a
sol_2 = (-b - math.sqrt(d))/2*a
#5
print("The value of x are {} and {}".format(sol_1,sol_2))
Explanation :
The commented numbers in the above program denote the step numbers below :
-
We are importing both cmath and math modules here. Because the discriminant(the part that is under the square root) may or may not be positive. If the discriminant is negative, the result will contain an imaginary part. For negative discriminant, we will use cmath.sqrt(), else_ math.sqrt()_ to find out the square root.
-
Ask the user to enter the values of a,b and c. Read and store them in different variables.
-
Calculate the discriminant using the user provided values.
-
Check if the value of the discriminant is negative or not. If yes, use the cmath.sqrt, else use math.sqrt to find out both solutions. We are storing the solutions in sol_1 and sol_2 variables.
-
Finally, print out the result to the user.
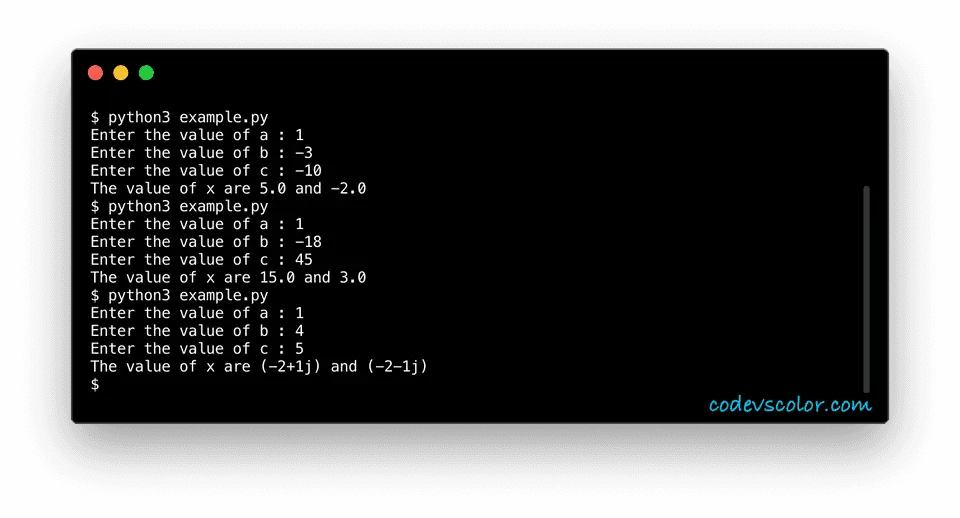
Sample Output :
Enter the value of a : 1
Enter the value of b : -3
Enter the value of c : -10
The value of x are 5.0 and -2.0
Enter the value of a : 1
Enter the value of b : -18
Enter the value of c : 45
The value of x are 15.0 and 3.0
Enter the value of a : 1
Enter the value of b : 4
Enter the value of c : 5
The value of x are (-2+1j) and (-2-1j)
As you can see, we have two solutions for all three examples. For the first and the second examples, we have real solutions and for the third one, we have an imaginary solution.
This example is also available on Github.