Implement bubble sort in C++

Implement bubble sort in C++:

Bubble sort is a sorting algorithm to sort one list or array. There are many other algorithms available to sort an array and bubble sort is one of these.

Bubble sort is a sorting algorithm and we can use this algorithm to write a program in any programming language that can sort an array.

In this post, we will learn how to sort the items of an array in C++.

How Bubble sort works:

Bubble sort is a comparison algorithm. It compares the adjacent elements of the array and swapped the elements to move the elements to the correct position.

On each iteration, it pushes the highest element to the end of the array. For the first iteration, it pushes the highest element to the end, for the second iteration, it pushes the second highest element to the end etc.

It keeps pushing the elements until the array is completly sorted.

Example of Bubble sort:

Let me show you one example of bubble sort with an array of numbers.

Suppose, we have the following array to sort:

[3, 11, 2, 12, 5]

Bubble sort algorithm will sort it in multiple iterations.

Iteration 1:

compare elements with indices 0 and 1. Since 3<11, move to next step.

[3, 11, 2, 12, 5] => [3, 11, 2, 12, 5]

compare elements with indices 1 and 2. Since 11>2, swap them.

[3, 11, 2, 12, 5] => [3, 2, 11, 12, 5]

compare elements with indices 2 and 3. Since 11<12, don’t do anything.

[3, 2, 11, 12, 5] => [3, 2, 11, 12, 5]

compare elements with indices 3 and 4. Since 12>5, swap them.

[3, 2, 11, 12, 5] => [3, 2, 11, 5, 12]

It will end the first iteration. You can see that the largest element is moved to the end.

Iteration 2:

compare elements with indices 0 and 1.

[3, 2, 11, 5, 12] => [2, 3, 11, 5, 12]

compare elements with indices 1 and 2.

[2, 3, 11, 5, 12] => [2, 3, 11, 5, 12]

compare elements with indices 2 and 3.

[2, 3, 11, 5, 12] => [2, 3, 5, 11, 12]

No need to compare numbers with indices 3 and 4 because we have already moved the largest value to index 4 in the first iteration. We will not move to the end in each iteration.

With the second iteration, the array is sorted. But, it will keep running for other iterations as well. The algorithm doesn’t know if it is sorted or not. So, it will run all 5 iterations and then it will stop.

Time and space complexity of bubble sort:

The space complexity is O(1), because we are not using any extra space to run it.

The time complexity is O(n) for best case scenario and O(n^2) for worst and average case.

The worst case will be if the array is already sorted. You have seen in the above example also, even if the array is sorted after two iteration, it keeps running.

Algorithm of Bubble sort:

The below algorithm we will use in the C++ program.

Take the numbers as input from the user and insert them to an array. Suppose, n is the total numbers.
Run one loop for n number of time. Let’s say we are using i for this loop and it runs from i = 0 to i = n - 1.
1. Run one inner loop for n - i number of time. Let’s say we are using j for this loop and it runs from j = 0 to j = n - i - 1.
2. Compare the elements at jth index with j+1th index. If jth item is greater than j+1th, swap them.
Print the array.

C++ program of bubble sort:

Below C++ program sorts an array using bubble sort. It takes the array values as inputs from the user and sorts the array using bubble sort.

#include <iostream>
using namespace std;

void bubbleSort(int *arr, int size)
{
  //5
  int temp;
  for (int i = 0; i < size - 1; i++)
  {
    //6
    for (int j = 0; j < size - i - 1; j++)
    {
      //7
      if (arr[j] > arr[j + 1])
      {
        temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }
  }
}

int main()
{
  //1
  int size;

  cout << "Enter the size of the array: " << endl;
  cin >> size;

  //2
  int arr[size];

  for (int i = 0; i < size; i++)
  {
    cout << "Enter item for index " << i << ": " << endl;
    cin >> arr[i];
  }

  //3
  bubbleSort(arr, size);

  //4
  cout << "Sorted Array: " << endl;
  for (int i = 0; i < size; i++)
  {
    cout << arr[i] << " ";
  }

  return 0;
}

Explanation:

The commented numbers in the above program denote the step numbers below:

size is an integer variable initialized to read the size of the array. This program is asking the user to enter the size. It reads that size and assigns it to size.
Create one array arr of size length. Using a for loop, reads the numbers from the user and add them to the array.
Call bubbleSort. bubbleSort function is used to sort the array using bubble sort. It takes the array and its size as the arguments.
Finally, print out the sorted array back using a for loop.
Inside bubbleSort, create one integer variable temp to use in swapping. Run two for loops as we discussed in the algorithm above. Inside the inner loop, if jth element is greater than j+1th element, swap their values.

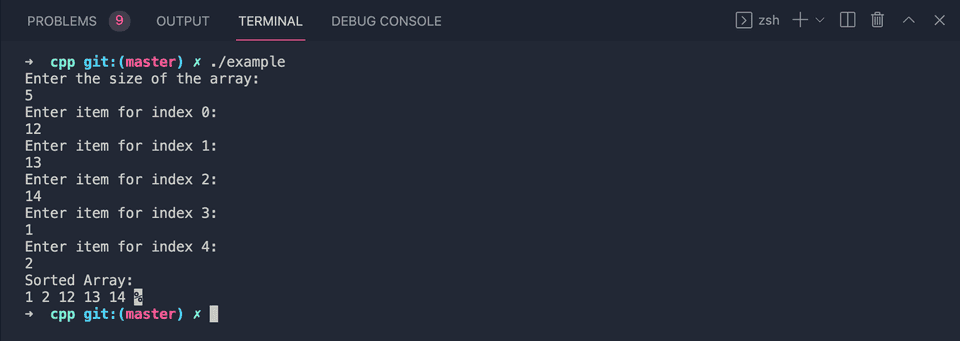
Sample output:

If you run the above program, it will print output as like below:

Enter the size of the array: 
5
Enter item for index 0: 
12
Enter item for index 1: 
13
Enter item for index 2: 
14
Enter item for index 3: 
1
Enter item for index 4: 
2
Sorted Array: 
1 2 12 13 14

Optimization of the bubble sort algorithm:

The time complexity for bubble sort is worst if the list is already sorted. Both loops will keep running even though the list is sorted.

We can optimize the original algorithm a little bit. We can initialize one flag as 1 and make sure that the outer loop will run only if this is 1.

This flag is assigned as 0 before the inner loop starts and if any swap is done, it is reassigned to 1.

So, if the inner loop doesn’t do any swap, i.e. if the list is sorted, the outer loop will not run again.

We can change the bubbleSort method as like below:

void bubbleSort(int *arr, int size)
{
  int temp;
  int swapped = 1;

  for (int i = 0; i < size - 1 && swapped == 1 ; i++)
  {
    swapped = 0;
 
    for (int j = 0; j < size - i - 1; j++)
    {
      if (arr[j] > arr[j + 1])
      {
        temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        swapped = 1;
      }
    }
  }
}

Here swapped acts as the flag we discussed above.

You might also like:

Updated on 16 Sep 2021

Journey with Code and DesignCodeVsColor on Twitter About
Privacy Policy
T&C
Contact