3 different C++ programs to find permutation and combination nPr and nCr

C++ program to find permutation and combination nPr and nCr :

This C++ program will show you how to find the permutation and combination of two user-provided values in three different ways. We need two values to find the permutation and combination. The total number of items and the items to pick on each selection.

A permutation is the number of ways we can arrange a given set of items and the order matters. Similarly, a combination is the number of ways we can select a given set of items without considering the order. If n is the total number of items of a set and r is the number of items to select on each subset, the permutation and combination are denoted by nPr and nCr respectively.

We will write one program that takes the values of n and r as inputs from the user and print out the calculated values.

Formula to find permutation and combination :

Before starting the program, let’s learn the formula to calculate the permutation and combinations.

As I explained before, permutation and combination are calculated by considering n distinct elements r at a time. So, we will take the values of n and r from the user. Below is the formula to find out a permutation:

nPr = n!/(n-r)!

Similarly, we can calculate the value of a combination with the below formula:

nCr = n!/r!(n-r)!

The symbol ! is used to define factorial.

As you can see, if we know how to find the factorial of a number, we can easily find out the nPr and nCr values of any two numbers.

How to calculate the factorial of a number:

We can calculate the factorial of a number in different ways. The factorial of a number is equal to the multiplication of all the positive numbers equal to or smaller than the number starting from 1. We have different ways to find the factorial of a number:

Iterative approach by using a loop:

• Initialize one variable as 1 to hold the final factorial result value.
• Run one loop from 1 to the number, by incrementing the value by 1 on each step.
• Multiply the value with the result on each step.
• At the end of the loop, the result will hold the factorial.

Recursive method:

We can also use a recursive method to find the factorial. It will call the same method again and again to calculate the factorial of a number.

Let’s learn how to use these methods to find the permutation and combination in C++.

Method 1: C++ program to find permutation and combination by using a for loop:

The following program uses a for loop to find the factorial of a number.

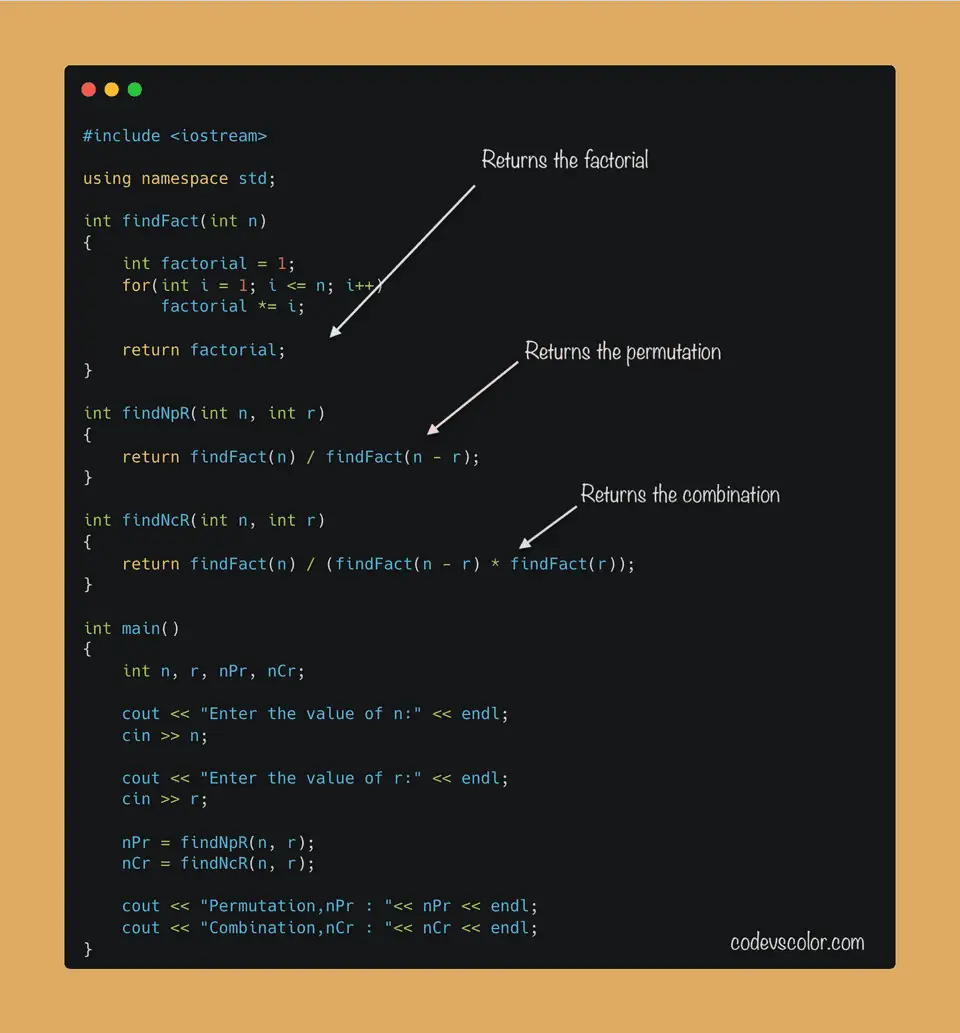
#include <iostream>

using namespace std;

int findFact(int n)
{
    int factorial = 1;
    for(int i = 1; i <= n; i++)
        factorial *= i;

    return factorial;
}

int findNpR(int n, int r)
{
    return findFact(n) / findFact(n - r);
}

int findNcR(int n, int r)
{
    return findFact(n) / (findFact(n - r) * findFact(r));
}

int main()
{
    int n, r, nPr, nCr;

    cout << "Enter the value of n:" << endl;
    cin >> n;

    cout << "Enter the value of r:" << endl;
    cin >> r;

    nPr = findNpR(n, r);
    nCr = findNcR(n, r);

    cout << "Permutation,nPr : "<< nPr << endl;
    cout << "Combination,nCr : "<< nCr << endl;
} 

Download this example on Github

• The findFact method finds the factorial of a number. It takes a number as its parameter and returns the factorial value.
  • It initializes a variable factorial as 1 to hold the factorial value of the number n.
  • The for loop runs from i = 1 to i = n. On each step, it increases the value of i by 1.
  • It returns the value of factorial.
• The findNpR method is used to calculate the permutation for the provided n and r values. Similarly, the findNcR method is used to calculate the combination.
• It takes the values of n and r as inputs from the user.
• It uses the findNpR and findNcR methods to calculate the permutation and combination of the user-provided numbers. These values are assigned to the nPr and nCr variables.
• The last two lines are used to print the calculated values.

This program will print outputs as below:

Enter the value of n:
12
Enter the value of r:
2
Permutation,nPr : 132
Combination,nCr : 66

Method 2: C++ program to find permutation and combination by using a while loop:

We can use a while loop to find the factorial of a number. Let me change the above example to use a while loop to calculate the factorial:

#include <iostream>

using namespace std;

int findFact(int n)
{
    int factorial = 1;
    int i = 1;

    while (i <= n)
    {
        factorial *= i;
        i++;
    }

    return factorial;
}

int findNpR(int n, int r)
{
    return findFact(n) / findFact(n - r);
}

int findNcR(int n, int r)
{
    return findFact(n) / (findFact(n - r) * findFact(r));
}

int main()
{
    int n, r, nPr, nCr;

    cout << "Enter the value of n:" << endl;
    cin >> n;

    cout << "Enter the value of r:" << endl;
    cin >> r;

    nPr = findNpR(n, r);
    nCr = findNcR(n, r);

    cout << "Permutation,nPr : " << nPr << endl;
    cout << "Combination,nCr : " << nCr << endl;
}

Download this example on Github

• The value of i is initialized before the loop starts. It will keep running until the value of i is smaller than or equal to i. On each step, we are multiplying the value of i with the variable factorial to calculate the required factorial.

It will print similar output.

Method 3: C++ program to find permutation and combination recursively:

This method will use a recursive method to find the permutation. This is more concise than the previous two methods:

#include <iostream>

using namespace std;

int findFact(int n)
{
    return n == 1 ? 1 : n * findFact(n - 1);
}

int findNpR(int n, int r)
{
    return findFact(n) / findFact(n - r);
}

int findNcR(int n, int r)
{
    return findFact(n) / (findFact(n - r) * findFact(r));
}

int main()
{
    int n, r, nPr, nCr;

    cout << "Enter the value of n:" << endl;
    cin >> n;

    cout << "Enter the value of r:" << endl;
    cin >> r;

    nPr = findNpR(n, r);
    nCr = findNcR(n, r);

    cout << "Permutation,nPr : "<< nPr << endl;
    cout << "Combination,nCr : "<< nCr << endl;
}

Download this example on Github

• The findFact method is a recursive method in this example.
• It returns n == 1 ? 1 : n * findFact(n - 1) i.e. if the current value of n is 1, it returns 1. Else, it returns n * findFact(n - 1) i.e. it recursively calls the same method with n - 1 as the parameter and multiplies the value with n. Similarly, findFact(n - 1) will return (n - 1) * findFact(n - 2) etc. and the recursive loop will stop when the value of the parameter will be 1.

You will get similar output with this example as well.

Enter the value of n:
10
Enter the value of r:
3
Permutation,nPr : 720
Combination,nCr : 120

You can try to run this application and find out permutations and combinations for different values.

You might also like:

• Singly linked list implementation in c++
• C++ linked list insert nodes to start and end
• C++ linked list example to delete a node
• How to reverse a linked list in C++
• C++ program to find the sum of first n natural numbers