C++ program to check if a number is Armstrong or not

Introduction :

In this C++ tutorial, we are going to learn how to check for an Armstrong number. A number is called an Armstrong number if the sum of its digits each raised to the power of the number of digits is equal to the number itself. (wiki).

If the number has only three digits, then the sum of the cubes of its digits is compared with the number. For example 371 is an Armstrong number because 33 + 73 + 1**3 = 371.

In this post, we will learn how to check if a number is Armstrong or not for a 3 digits number and for an n digit number.

Check Armstrong for a 3 digit number :

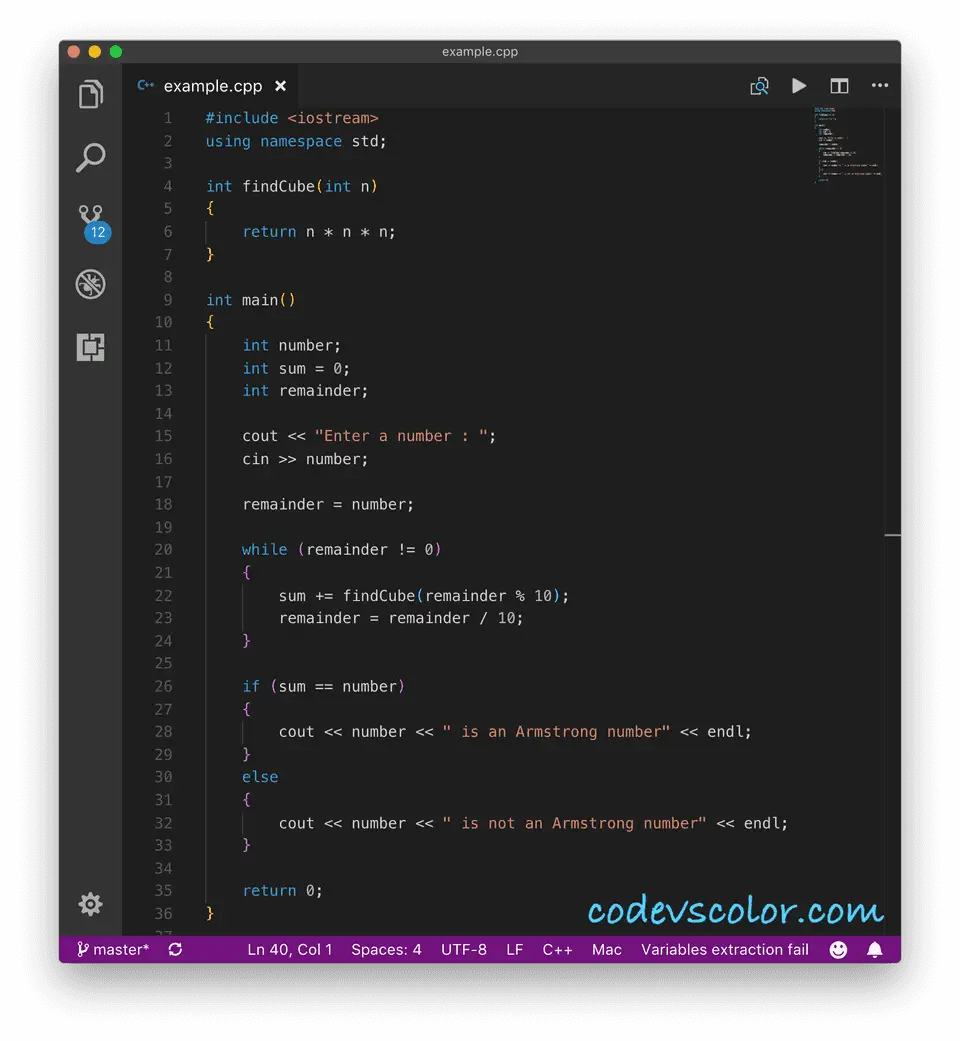
In this program, we will check if a number is Armstrong or not. This program is only for three digit numbers i.e. it will check if the number is equal to the sum of cubes of all digits of the number or not.

#include <iostream>
using namespace std;

//1
int findCube(int n)
{
    return n * n * n;
}

int main()
{
    //2
    int number;
    int sum = 0;
    int remainder;

    //3
    cout << "Enter a number : "; cin >> number;

    //4
    remainder = number;

    //5
    while (remainder != 0)
    {
        sum += findCube(remainder % 10);
        remainder = remainder / 10;
    }

    //6
    if (sum == number)
    {
        cout << number << " is an Armstrong number" << endl;
    }
    else
    {
        cout << number << " is not an Armstrong number" << endl;
    }

    return 0;
}

Explanation :

The commented numbers in the above program denote the step numbers below :

findCube is a function to get the cube of a number. It takes one integer as the parameter and returns its cube value.
Create three integer variables. number is for holding the user given number, the sum is for holding the sum of all cube of its digits and remainder is for holding the remainder value in the program.
Ask the user to enter the number. Read and store it in number variable.
Assign the value of the number to the remainder. At the start of the program, remainder and number will hold the same user input value.
Run one while loop until the value of remainder becomes 0. Inside the loop, it will add the rightmost digit of the remainder to the sum, and change the value of remainder to remainder/10.
Once the sum is calculated, it will compare it with number. If both are equal, it is an Armstrong number, else it is not.

For example, if the number is 123 :

First Iteration : sum = 0 + findCube(3) = 27, remainder = 123/10 = 12
Second Iteration : sum = 27 + findCube(2) = 8, remainder = 12/10 = 1
Third Iteration : sum = 35 + findCube(1) = 1, remainder = 1/10 = 0
Exit from the loop

So, the value of sum is 36 at the end of the loop for this example.

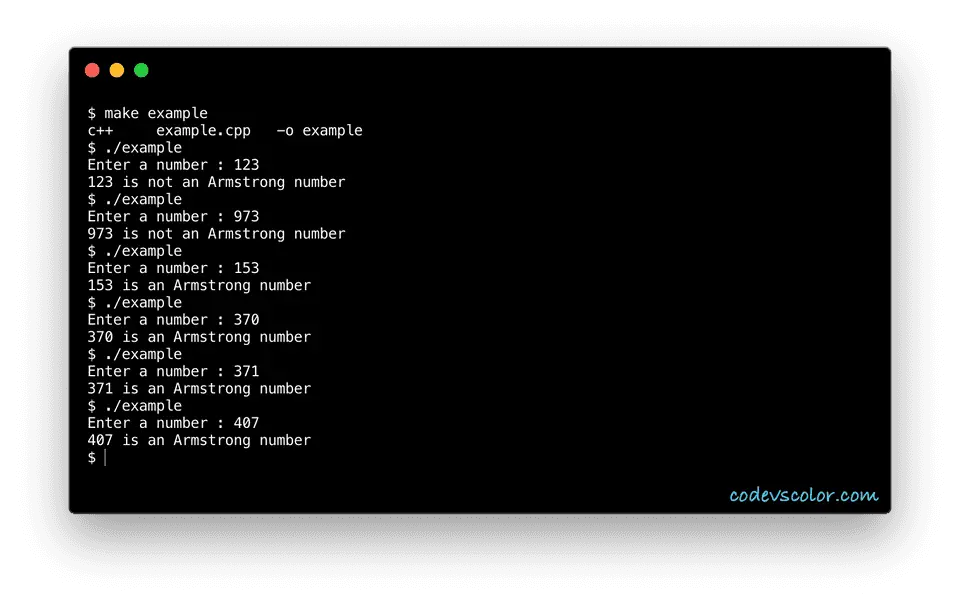
Sample Output :

Enter a number : 123
123 is not an Armstrong number

Enter a number : 973
973 is not an Armstrong number

Enter a number : 153
153 is an Armstrong number

Enter a number : 370
370 is an Armstrong number

Enter a number : 371
371 is an Armstrong number

Enter a number : 407
407 is an Armstrong number

Find Armstrong for any digit number :

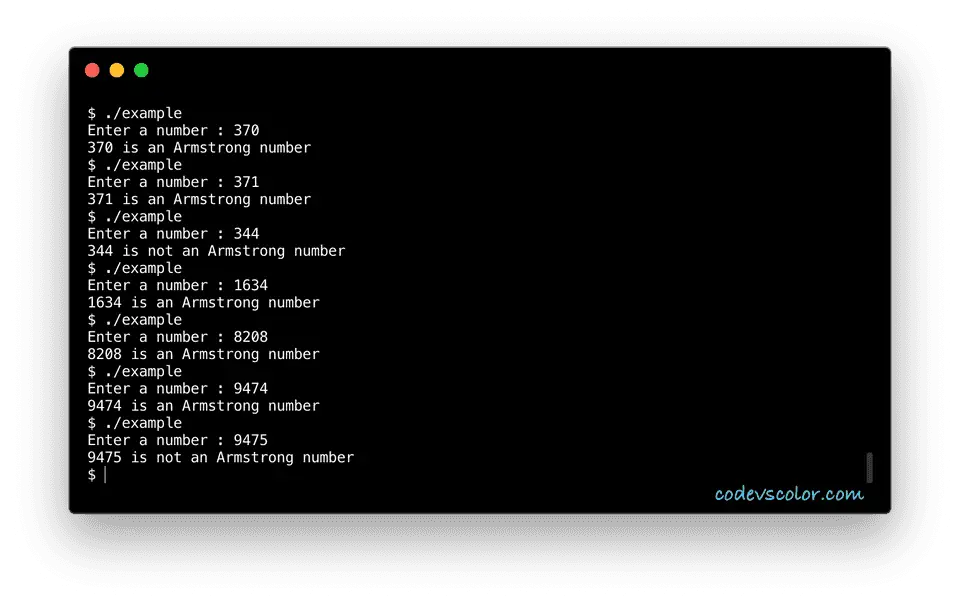
For a number with more than or less than 3 digits, we can use the same approach above. We need only to change the findCube function to find the power to any number n for an integer.

To do that, remove the findCube function and add the below function :

int findPower(int number, int digit)
{
    int remainingNumber = number;
    int result = 1;

    while (remainingNumber != 0)
    {
        result = result * digit;
        remainingNumber = remainingNumber / 10;
    }
    return result;
}

And call it like below inside the while loop :

sum += findPower(number, remainder % 10);

That’s it. It will find the power of a number to the total digits of that number. For example, 1634, 8208, 9474 are Armstrong numbers of four digits.

CodeVsColor