Pascal’s triangle in C program:
Pascal’s triangle is a triangle where each entry is the sum of the two numbers directly above it. This is a symmetric triangle, i.e. the left side numbers are identical to the right side numbers. Below is a pascal’s triangle of height 10 :
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
In this tutorial, we will learn how to print Pascal’s triangle in C program. The program will take the height as an input from the user and print it out.
Algorithm to print it :
It looks complex, but if you do understand the algorithm properly, you can write a program. Let’s divide the problem :
- We need to print numbers
- We need to print blank spaces
Consider one small triangle of height 5 :
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
If we print * instead of blank space, it will look like :
****1
***1*1
**1*2*1
*1*3*3*1
1*4*6*4*1
Here, height = 5
- for row = 1, total number of elements = 5, number is printed on position 5
- for row = 2, total number of elements = 6, number is printed on position 4,6
- for row = 3, total number of elements = 7, number is printed on position 3,5,7
- for row = 4, total number of elements = 8, number is printed on position 2,4,6,8
- for row = 5, total number of elements = 5, number is printed on position 1,3,5,7,9
so,
- The program will start i from 1 to rows
- j will run from 1 to i + rows - 1
- If the total number of elements is odd, the numbers are also odd. Else these are even.
- If the value of j is greater than or equal to rows - i, we are starting to print numbers.
- One blank space is printed between two numbers.
The nth entry of Pascal’s triangle for row is :
row! / (n! * (row - n)!);
C program :
The complete C program to print the pascal triangle is as below :
#include <stdio.h>
long findFactorial(long);
long findEntry(long, long);
void printEntry(long);
int main()
{
long rows;
long i, j, current;
long entry;
printf("Enter the number of rows : \n");
scanf("%ld", &rows);
for (i = 1; i <= rows; i++)
{
current = 0;
for (j = 1; j <= i + rows - 1; j++) { if ((i + rows - 1) % 2 != 0) { if (j >= (rows - i) && j % 2 != 0)
{
printEntry(findEntry(i - 1, current));
current++;
}
else
{
printf(" ");
}
}
else
{
if (j >= (rows - i) && j % 2 == 0)
{
printEntry(findEntry(i - 1, current));
current++;
}
else
{
printf(" ");
}
}
}
printf("\n");
}
return 0;
}
void printEntry(long value)
{
if (value < 10)
{
printf(" %ld", value);
}
else if (value < 100)
{
printf(" %ld", value);
}
else
{
printf("%ld", value);
}
}
long findEntry(long row, long position)
{
return findFactorial(row) / (findFactorial(position) * findFactorial(row - position));
}
long findFactorial(long n)
{
if (n == 0)
{
return 1;
}
else
{
return n * findFactorial(n - 1);
}
}
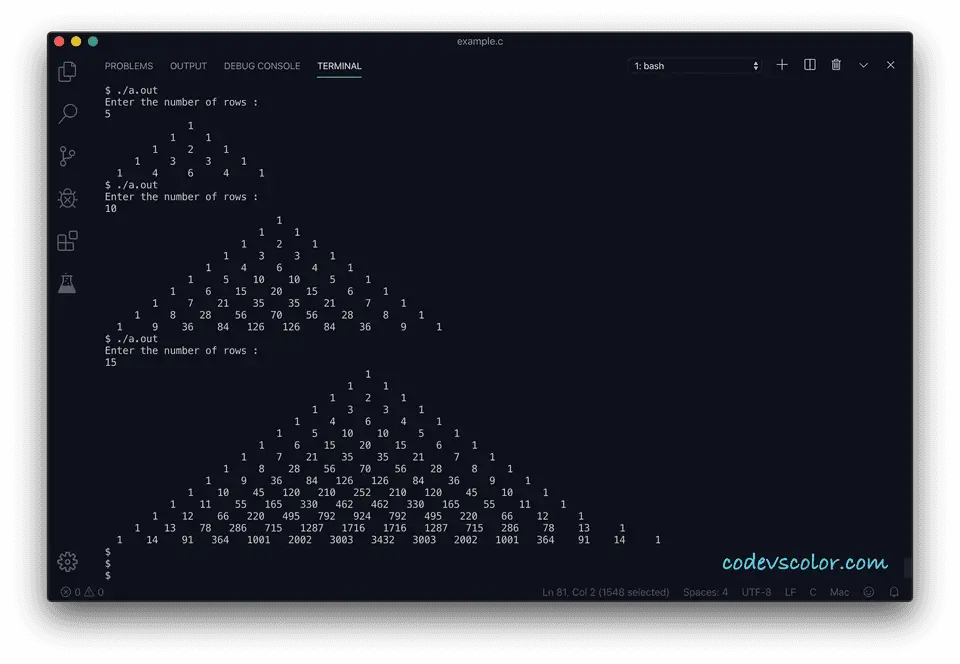
Sample Output :
Enter the number of rows :
5
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Enter the number of rows :
10
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
Enter the number of rows :
15
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
Note that the triangle will not print properly if the height is very high. We are using long and it will overflow the length of long.